Korelasi dalam ilmu statistik merupakan suatu metode pengukuran untuk melihat adanya kekuatan, bentuk arah, serta besarnya hubungan antar variabel. Dalam penerapan kehidupan sehari-hari, korelasi digunakan untuk mengetahui erat atau tidaknya hubungan antarvariabel. Jika hubungannya kuat dapat dilakukan suatu keputusan yang berguna. Dalam postingan kali ini saya akan membahas mengenai bagaimana cara menghitung serta mengintepretasikan koefisien korelasi Pearson Product Moment.
Sebenarnya, korelasi Pearson Product Moment merupakan nama lain dari metode korelasi sederhana atau simple linear correlation. Korelasi Pearson Product Moment atau biasa disebut dengan korelasi sederhana merupakan teknik korelasi yang digunakan untuk mengukur kekuatan dan arah hubungan 2 variabel yang linear. Dalam ilmu statistik, korelasi biasa disimbolkan dengan ρ untuk populasi dan r untuk sampel.
Definisi Korelasi Pearson Product Moment
Ukuran korelasi ρ linear diantara dua variabel x (independen) dan y (dependend) diduga dengan sampel koefisien korelasi r yang dirumuskan sebagai berikut:
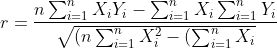^{2})(n\sum_{i=1}^{n}Y_{i}^{2}-(\sum_{i=1}^{n}Y_{i})^{2})}})
Nilai koefisien korelasi berada diantara -1 hingga 1
Dasarnya dalam korelasi Pearson Product Moment hanya digunakan untuk 2 variabel saja. Jika lebih dari dua variabel maka dapat digunakan dengan menggunakan korelasi berganda atau dengan menggunakan pendekatan analisis ragam.
Makna Koefisien Korelasi
Sebelum itu berdasarkan definisi korelasi, hasil koefisien korelasi memiliki beberapa makna ditinjau dari 2 segi. Yaitu segi arah dan kekuatannya. Tentu saja makna dari koefisien korelasi memberikan informasi bagi kita bagaimana hubungan antar dua variabel tersebut.
Ditinjau dari segi arah korelasi, apabila hasil koefisien korelasi bernilai positif maka memiliki dua arti. Yaitu:
Apabila hasil koefisien korelasi bernilai negatif maka memiliki dua arti pula. Yaitu:
Ditinjau dari segi kekuatan korelasi, dilihat dari interval koefisien korelasi berada. Apabila hasil nilai absolut (mutlak) koefisien korelasinya adalah 0 maka tidak ada hubungan. Namun apabila hasil absolut koefisien korelasinya adalah 1 maka hubungannya sempurna. Lebih jelasnya dapat dilihat dalam tabel berikut:
Dalam scatter plot, arah korelasi ditunjukkan dengan pola titik pencaran yang mengarah diagonal naik atau turun. Apabila pola titik pencarannya mengarah horizontal, diagonal, atau menyebar berbentuk lingkaran maka ada kemungkinan besar korelasi tersebut tidak memiliki arah. Kekuatan korelasi ditunjukkan dengan pola penyebaran titik yang mendekati suatu garis linear atau tidak. Apabila pola penyebaran titik membentuk dan mendekati garis linear maka korelasi tersebut memiliki hubungan yang kuat. Apabila pola penyebaran titik membentuk dan menjauhi garis linear maka korelasi tersebut memiliki hubungan yang lemah.
Contoh Soal 1:
Berikut ini merupakan data perusahaan mengenai harga permintaan suatu komoditi (X) dan harga rata-rata suatu komoditi (Y) disajikan dalam tabel berikut:
Hitunglah koefisien korelasi pada kasus tersebut dan bagaimana arti dari hasil koefisien korelasi yang didapat!
Jawaban Soal 1:
Berikut ini hasil perhitungan tabel untuk mendapatkan nilai total untuk X, Y, X2, Y2, dan XY:
Dengan memasukan nilai total dari semua variabel pada tabel dan jumlah data ke dalam rumus korelasi Pearson Product Moment maka didapat hasil sebagai berikut:
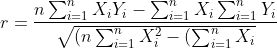^{2})(n\sum_{i=1}^{n}Y_{i}^{2}-(\sum_{i=1}^{n}Y_{i})^{2})}})
-(2400)(1420)}{\sqrt{(10(604072)-(2400)^{2})(10(207950)-(1420)^{2})}})
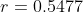
Maka nilai koefisien korelasi Pearson Product Momentnya adalah 0.5477. Bagaimana intepretasi arti dari hasil koefisien korelasi Pearson Product Moment pada kasus tersebut?
Koefisien Korelasi antara permintaan suatu komoditi dengan harga rata-rata komoditi sebesar 0.5477 dengan hubungan antara permintaan suatu komoditi dengan harga rata-rata komoditi memiliki tingkat hubungan yang menengah sehingga terkadang apabila ditambahkan permintaan suatu komoditi maka akan mempengaruhi peningkatan harga rata-rata suatu komoditi. Apabila diturunkan permintaan suatu komoditi maka akan mempengaruhi penurunan harga rata-rata suatu komoditi.
Dapat juga dibalik intepretasinya, apabila ditambahkan harga rata-rata suatu komoditi maka akan mempengaruhi peningkatan permintaan suatu komoditi. Apabila diturunkan harga rata-rata suatu komoditi maka akan mempengaruhi permintaan suatu komoditi.
Contoh Soal 2:
Diketahui data rekap data hasil pendapatan perusahaan (Y) berdasarkan jumlah sales (X1) dan harga yang dijual (X2) dengan masing-masing koefisien korelasi antar variabel yang didapat sebagai berikut:
rx1x2 = -0.545
rx1y = 0.986
rx2y = 0.436
Intepretasikan hasil koefisien korelasi berdasarkan informasi yang didapat dari kasus tersebut!
Jawaban Soal 2:
Ya itulah perhitungan dan cara mengintepretasikan hasil koefisien korelasi Pearson Product Moment dari suatu kasus. Demikian materi postingan tentang cara menghitung dan mengintepretasikan hasil koefisien korelasi Pearson Product Moment. Semoga bermanfaat.
Sebenarnya, korelasi Pearson Product Moment merupakan nama lain dari metode korelasi sederhana atau simple linear correlation. Korelasi Pearson Product Moment atau biasa disebut dengan korelasi sederhana merupakan teknik korelasi yang digunakan untuk mengukur kekuatan dan arah hubungan 2 variabel yang linear. Dalam ilmu statistik, korelasi biasa disimbolkan dengan ρ untuk populasi dan r untuk sampel.
Definisi Korelasi Pearson Product Moment
Ukuran korelasi ρ linear diantara dua variabel x (independen) dan y (dependend) diduga dengan sampel koefisien korelasi r yang dirumuskan sebagai berikut:
Nilai koefisien korelasi berada diantara -1 hingga 1
Dasarnya dalam korelasi Pearson Product Moment hanya digunakan untuk 2 variabel saja. Jika lebih dari dua variabel maka dapat digunakan dengan menggunakan korelasi berganda atau dengan menggunakan pendekatan analisis ragam.
Makna Koefisien Korelasi
Sebelum itu berdasarkan definisi korelasi, hasil koefisien korelasi memiliki beberapa makna ditinjau dari 2 segi. Yaitu segi arah dan kekuatannya. Tentu saja makna dari koefisien korelasi memberikan informasi bagi kita bagaimana hubungan antar dua variabel tersebut.
Ditinjau dari segi arah korelasi, apabila hasil koefisien korelasi bernilai positif maka memiliki dua arti. Yaitu:
- Apabila nilai variabel ditingkatkan, maka akan meningkatkan nilai variabel yang lain
- Apabila nilai variabel diturunkan, maka akan menurunkan nilai variabel yang lain
Apabila hasil koefisien korelasi bernilai negatif maka memiliki dua arti pula. Yaitu:
- Apabila nilai variabel ditingkatkan, maka akan menurunkan nilai variabel yang lain
- Apabila nilai variabel diturunkan, maka akan meningkatkan nilai variabel yang lain
Ditinjau dari segi kekuatan korelasi, dilihat dari interval koefisien korelasi berada. Apabila hasil nilai absolut (mutlak) koefisien korelasinya adalah 0 maka tidak ada hubungan. Namun apabila hasil absolut koefisien korelasinya adalah 1 maka hubungannya sempurna. Lebih jelasnya dapat dilihat dalam tabel berikut:
| Selang Koefisien Korelasi | Kekuatan Hubungan |
|---|---|
| |r| = 0.0 | Tidak ada hubungan |
| 0.0 < |r| < 0.2 | Sangat Lemah |
| 0.2 ≤ |r| < 0.4 | Lemah |
| 0.4 ≤ |r| < 0.6 | Moderate atau Sedang |
| 0.6 ≤ |r| < 0.8 | Kuat |
| 0.8 ≤ |r| < 1.0 | Sangat Kuat |
| |r| = 1.0 | Sempurna |
Dalam scatter plot, arah korelasi ditunjukkan dengan pola titik pencaran yang mengarah diagonal naik atau turun. Apabila pola titik pencarannya mengarah horizontal, diagonal, atau menyebar berbentuk lingkaran maka ada kemungkinan besar korelasi tersebut tidak memiliki arah. Kekuatan korelasi ditunjukkan dengan pola penyebaran titik yang mendekati suatu garis linear atau tidak. Apabila pola penyebaran titik membentuk dan mendekati garis linear maka korelasi tersebut memiliki hubungan yang kuat. Apabila pola penyebaran titik membentuk dan menjauhi garis linear maka korelasi tersebut memiliki hubungan yang lemah.
 |
| Scatter Plot Korelasi serta Artinya |
Contoh Soal 1:
Berikut ini merupakan data perusahaan mengenai harga permintaan suatu komoditi (X) dan harga rata-rata suatu komoditi (Y) disajikan dalam tabel berikut:
| X | Y |
|---|---|
| 178 | 105 |
| 224 | 105 |
| 160 | 130 |
| 315 | 130 |
| 229 | 130 |
| 250 | 150 |
| 181 | 150 |
| 306 | 170 |
| 257 | 170 |
| 300 | 180 |
Hitunglah koefisien korelasi pada kasus tersebut dan bagaimana arti dari hasil koefisien korelasi yang didapat!
Jawaban Soal 1:
Berikut ini hasil perhitungan tabel untuk mendapatkan nilai total untuk X, Y, X2, Y2, dan XY:
| Data | X | Y | X2 | Y2 | XY |
|---|---|---|---|---|---|
| 1 | 178 | 105 | 31684 | 11025 | 18690 |
| 2 | 224 | 105 | 50176 | 11025 | 23520 |
| 3 | 160 | 130 | 25600 | 16900 | 20800 |
| 4 | 315 | 130 | 99225 | 16900 | 40950 |
| 5 | 229 | 130 | 52441 | 16900 | 29770 |
| 6 | 250 | 150 | 62500 | 22500 | 37500 |
| 7 | 181 | 150 | 32761 | 22500 | 27150 |
| 8 | 306 | 170 | 93636 | 28900 | 52020 |
| 9 | 257 | 170 | 66049 | 28900 | 43690 |
| 10 | 300 | 180 | 90000 | 32400 | 54000 |
| Total | 2400 | 1420 | 604072 | 207950 | 348090 |
Dengan memasukan nilai total dari semua variabel pada tabel dan jumlah data ke dalam rumus korelasi Pearson Product Moment maka didapat hasil sebagai berikut:
Maka nilai koefisien korelasi Pearson Product Momentnya adalah 0.5477. Bagaimana intepretasi arti dari hasil koefisien korelasi Pearson Product Moment pada kasus tersebut?
Koefisien Korelasi antara permintaan suatu komoditi dengan harga rata-rata komoditi sebesar 0.5477 dengan hubungan antara permintaan suatu komoditi dengan harga rata-rata komoditi memiliki tingkat hubungan yang menengah sehingga terkadang apabila ditambahkan permintaan suatu komoditi maka akan mempengaruhi peningkatan harga rata-rata suatu komoditi. Apabila diturunkan permintaan suatu komoditi maka akan mempengaruhi penurunan harga rata-rata suatu komoditi.
Dapat juga dibalik intepretasinya, apabila ditambahkan harga rata-rata suatu komoditi maka akan mempengaruhi peningkatan permintaan suatu komoditi. Apabila diturunkan harga rata-rata suatu komoditi maka akan mempengaruhi permintaan suatu komoditi.
Contoh Soal 2:
Diketahui data rekap data hasil pendapatan perusahaan (Y) berdasarkan jumlah sales (X1) dan harga yang dijual (X2) dengan masing-masing koefisien korelasi antar variabel yang didapat sebagai berikut:
rx1x2 = -0.545
rx1y = 0.986
rx2y = 0.436
Intepretasikan hasil koefisien korelasi berdasarkan informasi yang didapat dari kasus tersebut!
Jawaban Soal 2:
- Untuk rx1x2 = -0.545 memiliki arti bahwa koefisien korelasi jumlah sales dengan harga jual sebesar -0.545 dengan arah hubungan yang negatif serta tingkat hubungan yang moderate, sehingga terkadang apabila jumlah sales ditingkatkan maka akan menurunkan harga jual. Sebaliknya terkadang apabila jumlah sales diturunkan maka akan meningkatkan harga jual.
- Untuk rx1y = 0.986 memiliki arti bahwa koefisien korelasi jumlah sales dengan pendapatan sebesar 0.986 dengan arah hubungan yang positif serta tingkat hubungan yang sangat kuat, sehingga jelas bahwa apabila jumlah sales ditingkatkan maka akan meningkatkan pendapatan. Sebaliknya jelas pula apabila jumlah sales diturunkan maka akan menurunkan pendapatan.
- Untuk rx2y = 0.436 memiliki arti bahwa koefisien korelasi harga jual dengan pendapatan sebesar 0.436 dengan arah hubungan yang positif serta tingkat hubungan yang moderate, sehingga terkadang apabila harga jual ditingkatkan maka akan meningkatkan pendapatan. Sebaliknya terkadang apabila harga jual diturunkan maka akan menurunkan pendapatan.
Ya itulah perhitungan dan cara mengintepretasikan hasil koefisien korelasi Pearson Product Moment dari suatu kasus. Demikian materi postingan tentang cara menghitung dan mengintepretasikan hasil koefisien korelasi Pearson Product Moment. Semoga bermanfaat.


0 Komentar untuk "Cara Menghitung dan Mengintepretasikan Korelasi Pearson Product Moment"